Task planning algorithm in TypeScript: real-life problem solved with a graph theory

In this article, I’ll present the algorithm which helps to answer the main question of all project planning efforts:

When will it be done?

A more formal representation of this problem sounds like: “Having some tasks which might depend on each other and some folks which can do those tasks when a milestone can be reached?”

Weekly sprint planning meeting in essence

A Little Backstory #

In 2019-2021 I work as a tech lead. I was responsible for 3 different projects with a team of 11 developers, 2 managers, 2 designers, and several departments to cooperate with.

For task tracking, we’re using our internal tool Yandex Tracker which is mostly like Jira. But it has no tools that’ll help to find the answer for an eternal question: “When?”. That’s why from time to time we manually sync tasks with Omniplan. Turned out that it’s the tool that solves almost all project planning problems and moreover it has an auto-planning feature so all situations when one assignee has workload over 100% are resolved automatically.

Still, it has some drawbacks:

So I’ve decided to try to make my own Omniplan version with blackjack and hookers that would be:

The most exciting part was to make a scheduling engine. I didn’t understand why only Omniplan has such an essential feature. Now I do.

So this article is about scheduling.

Developing a scheduling engine #

First I’ve done some research. I’ve googled for solving scheduling tasks in general and found a lot of about Gantt, PERT, but haven’t found any practical algorithms.

Then I looked for open-source libraries and found only one: Bryntum Chronograph. It seems like something I was looking for all the time. They even have benchmarks. But, well, talking honestly I didn’t understand any of its code and almost complete lack of documentation didn’t help either. I thought maybe, what if I could write it from scratch with less code.

So, as usual, I’ve tried to draw the problem.

Timeline of tasks before scheduling
Timeline of tasks before scheduling

While drawing it I’ve probably got the most important insight: tasks can be represented as a directed graph and edges are not only the explicit dependencies but also implicit dependencies by the same assignee.

The following algorithm should lead to such tasks arrangement:

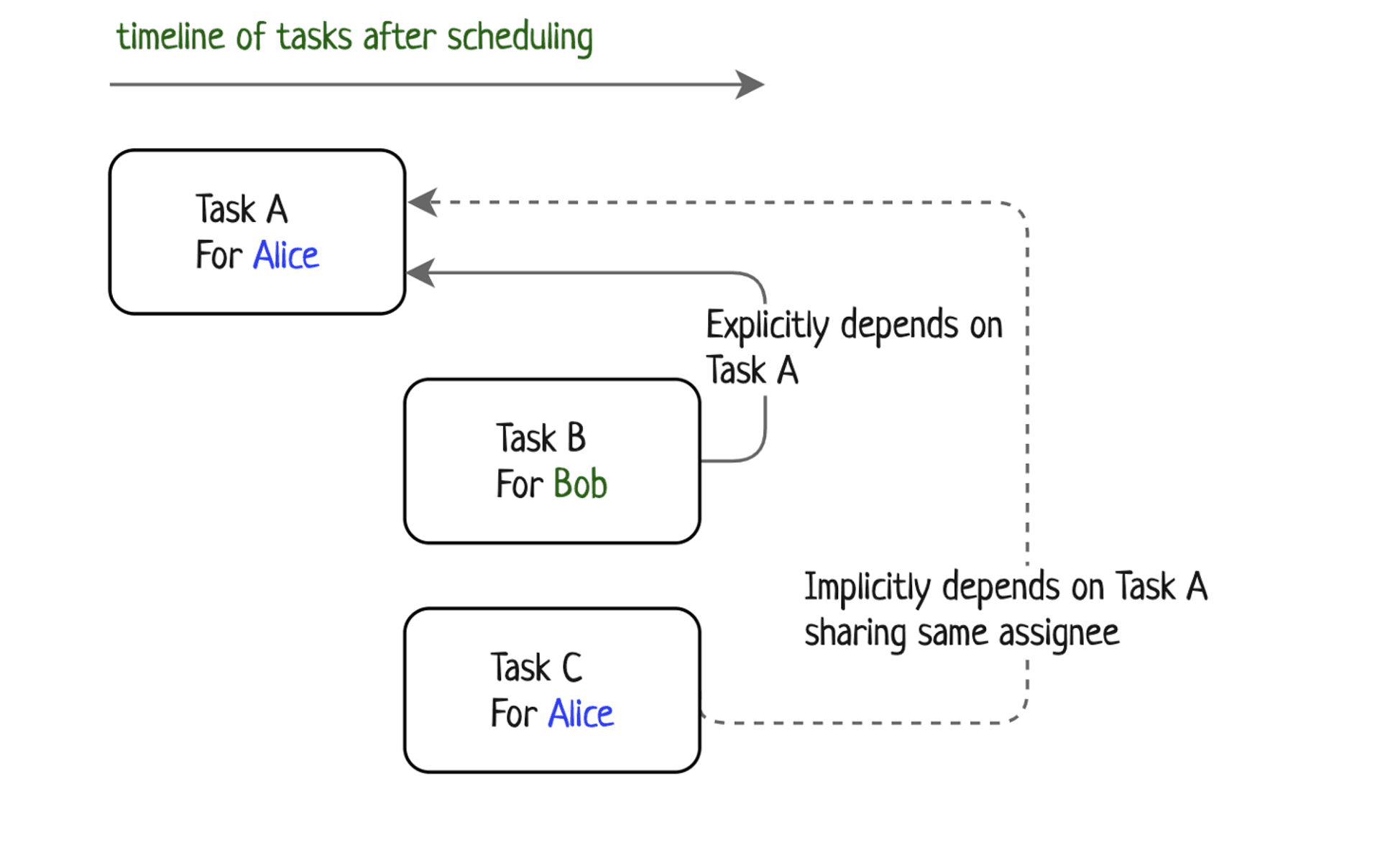
Timeline of tasks after scheduling
Timeline of tasks after scheduling

Let’s consider what a task is:

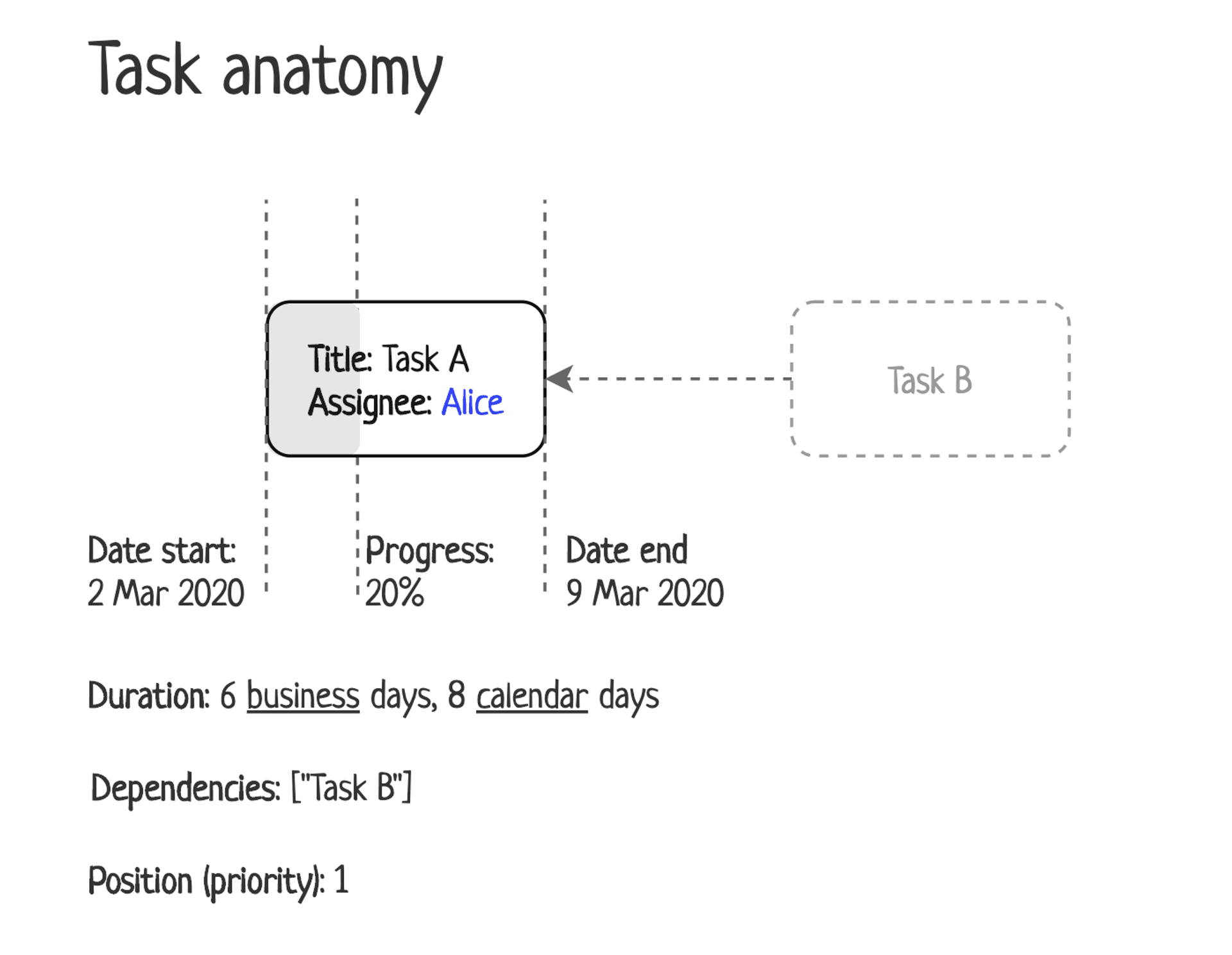
Task anatomy
Task anatomy

There are some not so obvious properties of a task:

So TypeScript type is as follows (ID is just an alias for string):

export type Task = {
  id: ID;
  title: string;
  start: Date;
  end: Date;
  duration: number;

  /**
   * Approximation of priority
   */
  position: number;
  progress: number;
  resourceId: ID;
  /**
   * Current task blocked by these tasks (depends on)
   */
  blockedBy?: Array<ID>;
};

The algorithm #

In essence, the algorithm should change start and end dates of the tasks in the following way:

  1. Tasks should start today if it is possible
  2. It should be impossible to start a task today if it has other tasks as prerequisites that are unfinished. In that case, a task should start right after the last prerequisite’s end date.

Pretty simple, huh? 🙈

The main steps of the algorithm are:

  1. Build a graph from tasks. Make edges taking into account explicit dependencies and implicit dependencies by the same assignee.
/**
 * Graph respects explicit dependencies
 * and implicit by resources (via positions)
 */
export const makeGraphFromTasks = (tasks: Array<Task>): Graph => {
  // task and blockedBy
  const graph: Graph = new Map();
  const resourcesTasks = new Map<ID, Array<Task>>();

  // Create graphs
  for (const t of tasks) {
    // resource and its tasks
    const tasksOfResource = resourcesTasks.get(t.resourceId) ?? [];
    tasksOfResource.push(t);

    resourcesTasks.set(t.resourceId, tasksOfResource);

    graph.set(t.id, new Set(t.blockedBy ?? []));
  }

  // Now add deps
  for (const tasksOfResource of resourcesTasks.values()) {
    // first sort by position so links of tasks starts with higher position
    // then topological sort to reduce cyclic deps
    tasksOfResource.sort((a, b) => a.position - b.position);
    // is toposort needed?
    const sortedTasks = toposort(graph, tasksOfResource);

    // add to graph such edges so current node has prev as dependency (blocked by prev)
    let prevTask: Task | void;
    for (const task of sortedTasks) {
      if (
        prevTask &&
        prevTask.id !== task.id &&
        // has no incoming edge as well (otherwise it will be cyclic dep)
        !graph.get(prevTask.id)?.has(task.id)
      ) {
        graph.get(task.id)?.add(prevTask.id);
      }
      prevTask = task;
    }
  }

  return graph;
};

2.Remove circular dependencies. If cycles are present throw an error because that means that some task A has as prerequisite task B and task B has as prerequisite task A, which is a classic problem of circular dependency and the problem should be resolved manually. Tasks A and B do not necessarily have an explicit dependency on each other, there are might some other tasks between them.

/**
 * Main source of cyclic dependencies is previous step where graph is created
 * Often top-level task has same owner as children tasks
 * Since we create edge in graph also by same owner that's why there is cyclic deps
 *
 * IDEA: mitigate the issue by starting DFS walk from top-level (source) tasks!
 */
export const removeCyclicDependencies = (
  graph: Graph,
  tasks: Array<Task>
): void => {
  // Track visited to avoid computing path for already computed nodes
  const visited = new Set();
  let cyclicDepsRemovedCount = 0;

  const dfsAndRemove = (rootTaskId: ID) => {
    // [current task ID, set of previously visited tasks]
    const stack: Array<[ID, Set<ID>]> = [[rootTaskId, new Set()]];

    while (stack.length > 0) {
      const nextValue = stack.pop();
      nullthrows(nextValue);
      const [taskId, prevSet] = nextValue;

      const blockedBy = graph.get(taskId) ?? new Set();

      visited.add(taskId);

      for (const blockedById of blockedBy) {
        // cycle detected!
        if (prevSet.has(blockedById)) {
          // remove that edge
          blockedBy.delete(blockedById);
          cyclicDepsRemovedCount++;
          continue;
        }

        const newPrevSet = new Set(prevSet);
        newPrevSet.add(blockedById);
        stack.push([blockedById, newPrevSet]);
      }
    }
  };

  for (const task of tasks) {
    if (visited.has(task.id)) {
      continue;
    }

    dfsAndRemove(task.id);
  }

  console.debug("Cyclic deps removed:", cyclicDepsRemovedCount);
};

3. Visit every node (task) and update a start and end dates. Visiting should be performed starting from the task with higher priority

If a task is a source (it is not a prerequisite for any other task and task’s assignee has no other task to do before this task) or a task is disconnected node (it has no dependencies and it is not prerequisite for any other tasks) then we start task today.

Otherwise, a task has prerequisites and its start date should be set to the latest end date of its prerequisites tasks.

Also, it is important to correctly update an end date while setting a start date of a task. We should take into account actual business days and the progress of a task.

export const scheduleTasks = (
  inputTasks: Array<Task>,
  today: Date = getNowDate()
): Array<Task> => {
  const dayBeforeToday = subtractDays(today, 1);
  const tasks: Array<Task> = inputTasks.map((t) => ({ ...t }));
  const tasksById: TasksById = Object.fromEntries(tasks.map((t) => [t.id, t]));
  const graph = makeGraphFromTasks(tasks);
  let cyclesToFullyUpdateDates = 1;

  // 1. Remove cyclic dependencies
  removeCyclicDependencies(graph, tasks);

  // 2. Initial update of all tasks start and ends days taking into account business days
  for (const task of tasks) {
    updateTaskDatesByStart(task, today, true);
  }

  // Repeat until dates remains unchanged, max graph.size times.
  // Similar to optimization in Bellman-Ford algorithm
  // @see https://en.wikipedia.org/wiki/Bellman–Ford_algorithm#Improvements
  for (let i = 0; i < tasks.length; i++) {
    let isAnyTaskTimelineChanged = false;

    for (const [taskId] of dfs(graph)) {
      const task = tasksById[taskId];
      // if blockedBy task not in initial data set
      if (task === undefined) {
        continue;
      }
      const blockedByTasks = Array.from(graph.get(task.id) ?? [])
        .map((blockedById) => tasksById[blockedById])
        // do not take into account tasks not in graph
        .filter(Boolean);
      const blockedByEndDates = blockedByTasks.map((t) => t.end);
      // add dayBeforeToday by default, so task without blockedBy starts on today
      blockedByEndDates.push(dayBeforeToday);

      // Start task on the next day after previous (blockedBy) tasks ends
      const maxBlockedByEndDate = addDays(maxDateTime(blockedByEndDates), 1);
      const isTaskTimelineUpdated = updateTaskDatesByStart(
        task,
        maxBlockedByEndDate
      );
      if (isTaskTimelineUpdated) {
        isAnyTaskTimelineChanged = true;
      }
    }

    if (isAnyTaskTimelineChanged === false) {
      break;
    }
    cyclesToFullyUpdateDates++;

    if (isAnyTaskTimelineChanged && i === tasks.length - 1) {
      console.error(
        'It\'s not enought "tasks.length" interations to fully schedule all tasks!'
      );
    }
  }

  console.debug(
    `Cycles to fully update dates ${cyclesToFullyUpdateDates}/${tasks.length}`
  );

  // for better representation
  return toposort(graph, tasks);
};

What can be improved #

  1. Probably the most important feature which leads to a more complex solution is introducing a desirable start date of a task. I didn’t research it yet, but if someday it will grow to a standalone web-service I think it should be done. Now, this feature can be mitigated by setting proper priorities of tasks.
  2. For the enterprise-grade solution, it is important to take into account vacations and public holidays. I think updateStartDate function can be quite easily updated to support this functionality.
  3. For my case having a day as a time quant was okay, but I believe for some people hour-based planning might be important. I think implementing an hour-based quant can also introduce some complications to code.

Conclusion #

The code from the article you can find here. You can grab and use it as an NPM package.

I’m wondering if a presented solution has some flaws. If you spotted some please contact me here or on issues section in Github.

#task planning #algorithms #typescript

***

Since you've made it this far, sharing this article on your favorite social media network would be highly appreciated 💖! For feedback, please ping me on Twitter.

Published